开关问题算法与游戏中的例子
在游戏《逃离方块:洞穴》中,有一个这样的谜题,如下图[1]所示:

谜题的规则如下:
- 每点击一根触角,这根触角上的吸盘会增加两个,与之相邻的触角上的吸盘会增加一个(如对于图中从左数第 2 的触角,点击后,从左数各触角的吸盘数量为:3、6、6、3)
- 如果触角上的吸盘已经满了,再增加就会全部清空,从零开始新增(如果点击图中左数第 2 个触角 3 下,则从左数各触角的吸盘数量为:5、2、1、3)
- 全部的触角上的吸盘都满了,则算作谜题得解
由此,我们可以认为,触角 1 的吸盘数是模 7 的(即满 7 后再增加从 0 开始,只是游戏中用“7”的状态代替“0”的状态而已),最终目标是使其数值等于 7(即0);同理,触角 2 就是模 8 的,以此类推。游戏的目标,是让所有触角的吸盘数,为各自模数集合中的 0。我们不妨设四个触角的点击数为 a,b,c,d,对于第一个触角,就有 2a + b = 5 mod 7,2a 表示点击自己对自己的吸盘数量增加值为 2,b 表示点击第二个触角对第一个触角的增加值为 1,最终的目标是填充缺少的 5 个吸盘,同时考虑到周期的情况,要加上模 7。其他触角同理,那么,可以列出方程:
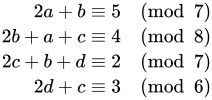
显然,这个方程组过于复杂,难以求通解,即便是用计算机来计算也不算容易。游戏设计者当然是不会要求玩家去解这样一个方程,而是通过其他策略解决。对于如何求解这个问题,我们暂时搁置,而是先探讨另一个很相似的算法领域的问题——开关问题。
01 开关问题
开关问题的基本定义是:有 N 个相同的开关,每个开关都与某些开关有着联系,每当你打开或者关闭某个开关的时候,其他的与此开关相关联的开关也会相应地发生变化,即这些相联系的开关的状态如果原来为开就变为关,如果为关就变为开。你的目标是经过若干次开关操作后使得最后 N 个开关达到一个特定的状态。[2]
这和上面的例子很像,只不过这里每个开关都只有“开”和“关”两个状态,是模 2 的。
这也有对应的游戏例子,如游戏《摩尔庄园》中的“警官任务”中就有类似的谜题[3]:

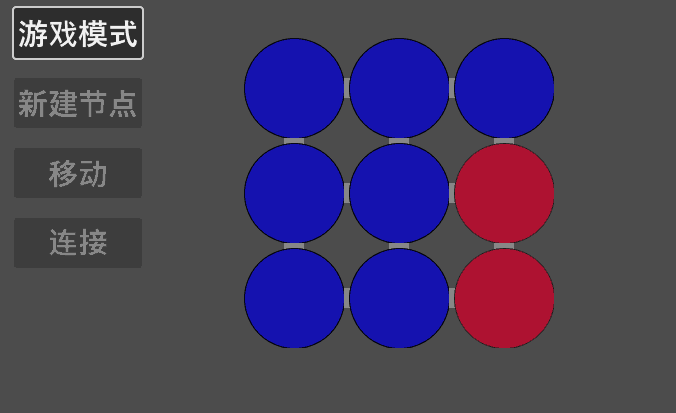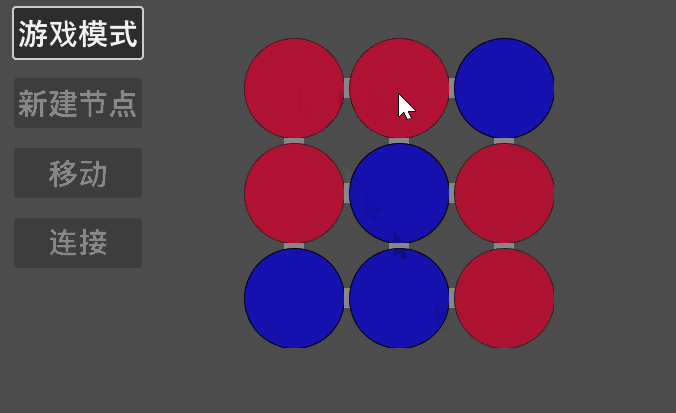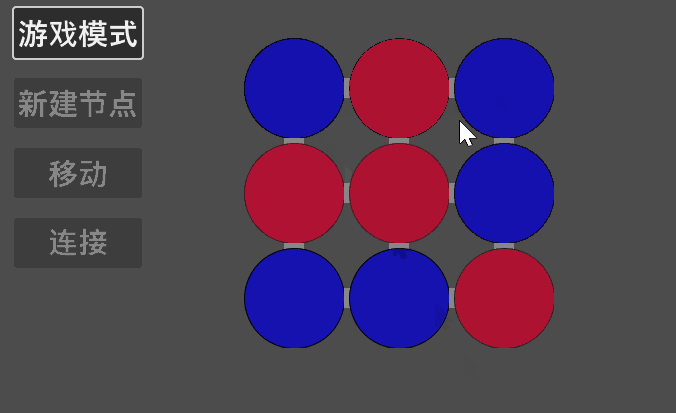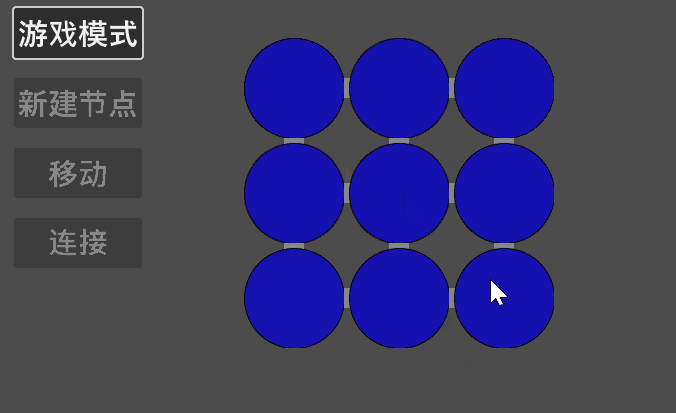
每一个圈都和与它上下左右四个方向的圈相连,点击一个圈会改变这个圈的颜色(红色/绿色),同时也改变与它相连的圈的颜色。把所有的圈都变成绿色,视作谜题得解。这本质上也还是求解同余方程组的问题,只不过参数是 9 个,开关是模 2 的而已。
在游戏《被错过的天堂》中,也有一样的谜题[4]:

此外,在《逃离方块:阿尔勒》中,也有一个相对更简单的“向日葵”开关解谜[5]:

与前面的解谜类似,点击左侧的向日葵花圈会变大,并使得与之相邻的花圈也变大;使得左侧所有的向日葵都是“变大”状态,右侧的向日葵就会升到最高,并提供后续所需的钥匙。
向日葵花圈之间的连接关系类似下面的节点图:
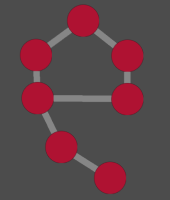
以这个谜题为例,可以效仿最开始的例子,列出如下的同余方程组(设节点从上到下、从左到右依次为 a ~ g):
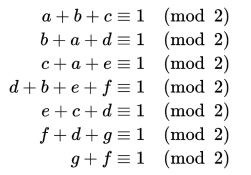
由于模均为 2,很容易想到另一种运算:异或。我们可以把上面的方程组看作是“每个方程的各变量必须有奇数个奇数”,如 a + b + c = 1 mod 2 就可以理解成 a,b,c 这三个数中,奇数应该有 1 个,或者 3 个都是,这就很容易用异或方程组来表示。
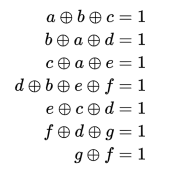
经过很简单的推算就可以得到答案(带入验证过程略):
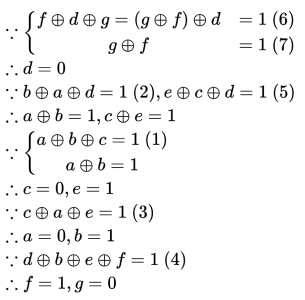
根据计算得到的结果,我们只需要依次点击第 2、第 5 和第 6 个节点,就可以解决该谜题。

当然,从程序的角度,我们更希望能够用某种通行的解法解题。对于线性方程组,我们可以将各参数和结果转换成增广矩阵,然后使用高斯消元法求解。异或方程组其实也一样,也可以转换成矩阵, 然后借用高斯消元的思想求解,且异或的计算要比线性方程更加简单。
我们可以先从基本的线性方程组求解入手,逐步过渡到异或方程组的求解。
02 从线性方程组到异或方程组
高斯消元法的原理和代码网络上已经有很多教程文章,这里不多赘述,给出一篇文章作为参考:高斯消元法详解-CSDN博客(内含高斯消元的优化代码)
一言以蔽之,线性方程组的高斯消元法的步骤为:确定列主元 -> 消元 -> 重复直到消完 -> 回代
这里用 Python 重写上述博客的 C++ 代码,并修复部分问题:
1 | |
由于异或方程组的值只有 0 和 1 两种可能,使用高斯消元的时候执行一步异或运算即可:
1 | |
我们可以将前面“向日葵”开关解谜的方程组转换为矩阵形式,并测试结果:
1 | |
输出的矩阵中,最右侧的一列分别为:0,1,0,0,1,1,0,即第 2,5,6 节点为 1,其余均为 0,这与我们之前手算的结果是一致的。
再测试《被错过的天堂》中的例子:
1 | |
即只需要点击(从上往下、从左往右数)第 1,2,3,5,9 个节点即可完成解谜。
这里使用 Godot 简单写了一个程序用于验证,可以看到,结果是正确的。
03 多元线性同余方程组
现在回到最开始的“章鱼”谜题,我们可以沿用这种高斯消元的方法去解决这样一个同余方程组吗?似乎不能。虽然异或方程组也可以视作是模 2 的线性方程组,但在异或方程组中,每一个方程的模都是一样的;也就是说,只能确保模相同的同余方程组可以用类似的方法解决。
这部分涉及到复杂的数论问题,超出了本人的知识范畴和研究能力。但就网络上大多数关于数论和线性同余方程的问题,也多集中于一元线性同余方程(组),以及模相同的多元线性同余方程组,鲜有对模不同的同余方程组的讨论。
对于一元线性同余方程组,通常可以使用中国剩余定理及更一般的数论公式求解[6]:

对于同模的多元线性同余方程组,因为处于同一数集,也可以用矩阵消元的方式求解。对于形如
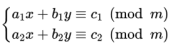
的方程组,可以先通过矩阵消元(消元时考虑数域即可)化简成
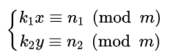
的形式,然后再对每个一元同余方程求解[7]。或者用不定参数表示模数,改写方程观察求解[8]。
然而,对于不同模的情况,似乎没法总结出一套系统的方案解决。苦于能力有限,为了快速的得到答案,这里放弃寻找通解,直接编写程序暴力求解最小可行值:
1 | |
使用 Godot 针对本案例专门写一个运行程序验证结果正确性,事实证明结果正确。

04 玩家如何解题?
前面都是使用算法和程序来解题,但这些方法的复杂程度过高。对于玩家而言,一套简单易学的通行的解决方案,比“题目有没有解”“通解怎么求”更重要。我们不可能要求玩家在玩游戏的时候看到谜题,第一反应不是去思考和尝试,而是拿出纸和笔甚至借助程序。
那么,能不能针对这类解谜,总结出一些解题技巧呢?应该也是可以的。就比如,对于《被错过的天堂》的九宫格节点模型,可以把这 9 个节点抽象成 3 类:角点、边点、中心点。
容易得到,点击所有的角点和中心点,可以让 9 个节点的状态都转换成相反的状态。所以,只要能够使所有节点的颜色变红,就能使得所有节点的颜色变蓝。
此外,与魔方类似,如果对于任意一个点,进行若干操作,可以使得这个点变化状态而其他各点不变,那么,我们就可以像复原魔方一样,完成这个解谜。经过程序验证,我们可以总结出以下三种最基本的情况:
- 使得“角点”单独改变状态:点击自己,和“对角点”水平方向、竖直方向的另外 4 个点,共 5 个点(如下图的案例,点击第 2,3,4,7,9 五个点;由于对称,其他“角点”同理)

- 使得“边点”单独改变状态:点击“对边点”,及与“对边点”相邻的其他 3 个点,共 4 个点(如下图的案例,点击第 1,4,5,7 四个点;由于对称,其他“边点”同理)

- 使得“中间点”单独改变状态:点击该“中间点”和四个“边点”即可(如下图的案例,点击第 2,4,5,6,8 五个点)

根据以上三个基本情况,就可以推导出所有情况下的解法。就像魔方公式一样,玩家只需要记住少量的公式,就可以应对所有的打乱情形。譬如用这三种情形应对《被错过的天堂》中的案例,只需要依次执行情形 1 和情形 2 的公式即可,即依次点击 2,3,4,7,9 和 1,4,5,7。考虑到重复的节点 4 和 7,去除后就是之前运算得到的解 1,2,3,5,9。
但这毕竟是一个非常“对称”的解谜模型,对于逃离方块系列的“向日葵”谜题和“章鱼”谜题,本身就比较特殊,总结出来的公式想必也会很复杂,还不如直接“硬碰硬”。
我们可以再针对“向日葵”谜题作讨论,感受一下复杂程度。省略过程和截图,通过计算机验证,结论如下(注意到节点 1 和 3 对称,节点 2 和 5 对称):
- 单独改变节点 1:3,5,6,7
- 单独改变节点 2:2,3,5
- 单独改变节点 3:1,2,6,7(类似 1,改变另一侧的节点 1,2)
- 单独改变节点 4:6,7
- 单独改变节点 5:1,2,5(类似 2,改变另一侧的节点 1)
- 单独改变节点 6:1,3,4,6,7
- 单独改变节点 7:1,3,4,6
足见公式很复杂,而且这些公式直接推非常麻烦,不如多尝试一会儿或拿出纸笔推算。“章鱼”谜题更不必说,对于大多数玩家而言,他们更倾向于尝试一种“保守的策略”,即:
- 从左往右数的第一根触角开始点击
- 若下一次点击会“清零”(即还差 1 个吸盘)时,转到下一根触角
- 若下一次点击会使得上一根触角(如果有的话)“清零”(即上一根触角的吸盘已经“满了”)时,转到下一条触角
- 如果当前是最后一根触角,反复点击,直到谜题解决
但这种策略是有问题的,我们可以把这种策略用在方程的特殊值测试上:

最后得到的方程组是无解的,因为 2d 作为一个偶数,除 6 后的余数一定也是偶数,不可能是 3。所以,这种策略不可行,最后不得不调整前面的节点。
然而,或许是逃离方块系列的制作组考虑到了这一点,对游戏的规则做了一点小小的改动:点击章鱼的一条触角,会先在自身和相邻的触角上先各增加一个吸盘,如果没有解题,再在自身上增加一各吸盘。这样,如果最后两根触角都只差一个吸盘,点击最后一根触角,也可以解题。如若使用上述策略,考虑这种情形,最后得到的方程组如下:
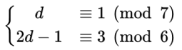
易得当 d = 8 时,满足条件。使用这种策略,可以解决该谜题。

这也给游戏制作者提供了启示:对于点击解谜游戏中的谜题设计,应该尽量简单,至少能够让玩家通过有限的推理得到答案,或者通过某种容易想到的策略可以解题。如果谜题的复杂性过高,或者难以通过有限的推理得出,那么玩家就不是在“解谜”而是在“猜谜”,这会极大的降低玩家游玩的意愿,而这显然不是游戏开发者愿意看到的。
游戏开发者可以选择像逃离方块系列一样,对游戏规则进行修改以降低难度,对玩家更友好。当然最好还是要避免这种谜题的出现,尽量选择一些玩家容易上手,可以通过简单的思考得出解法的谜题(如数独、数织、简单的华容道等),而不是像开关问题这样稍微复杂就“抓瞎”的类型。
参考/引用内容
- 素材来自13-逃离方块:洞穴(上)_哔哩哔哩_bilibili ↩
- 介绍引用自开关问题(高斯消元,异或方程组) - Ym2011 的博客 - 洛谷博客 (luogu.com.cn) ↩
- 素材来自【摩尔庄园】摩尔警官任务:古董失窃案通关-攻略向_哔哩哔哩_bilibili ↩
- 素材来自【怀旧向】《被错过的天堂》双结局流程视频_哔哩哔哩bilibili ↩
- 素材来自05-逃离方块:阿尔勒(番外)_哔哩哔哩_bilibili ↩
- 截自文章初等数论笔记Part 2:中国剩余定理 - 知乎 ↩
- 参考了回答有无大神详细说一下怎么用高斯消元法解这个线性同余方程组? - 知乎 (zhihu.com) ↩
- 参考了论坛Solving linear congruence classes - Mathematics Stack Exchange ↩